이등변 삼각형의 면적을 찾는 법

특히 수학, 기하학에 따라학생의 여론 조사, 가장 익숙하지 않은 수업 중 하나, 그리고 모두 그들이 현재 성인의 90 %가 실용적인 응용 프로그램을 찾지 못했던 수많은 수식을 배우게하기 때문에. 하지만 잠깐 동안 수식을 배우고 문제를 해결하며 인생에서 우리에게 유용 할 수있는 것이 아니라 사고와 논리를 발전시키기 때문에 방정식을 만듭니다. 심지어 고대 그리스 현자들도 인간의 지성은 수학 과학에 대한 지식으로 측정 할 수 있다고 말했다. 그리고 당신이 이등변 삼각형에 대한 공식 적용에 익숙해지기로 결정했기 때문에 우리는 스스로를 가지고 전체 기사를 읽었습니다.
질문에 대답하기 전에 찾기 방법이등변 삼각형의 면적과 수식과 계산이 주어진 기사의 실용적인 부분으로 가면, 우리 자신을위한 바로 그 개념을 나타냅니다. 이등변 삼각형은 3 개의 변 중 2 개의 변이 길이가 같은 삼각형입니다. 모든면이 같은 정삼각형의 경우 이등변 삼각형이 올바른 것으로 간주 될 때 이등변 삼각형으로 간주되지만 그 반대의 경우는 틀립니다.
삼각형의 변을 지정해야합니다. 아래 그림과 같이이 방법을 사용합니다. a - sides, b-base 및 h-height.
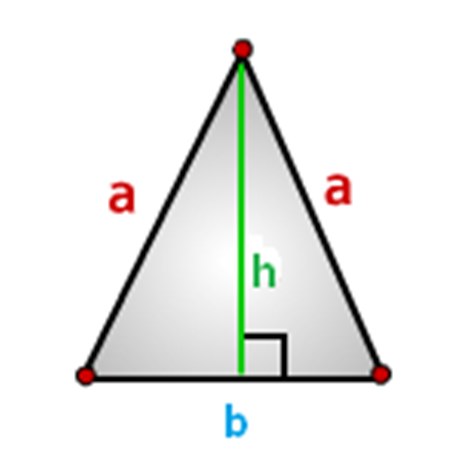
이등변 삼각형, 수식의 면적을 계산하는 방법.
우리가 높이, 측면 및 각을 표기 한 후에 우리는 문제를 해결하기 시작할 수 있습니다.
우선, 우리가 아는 것을 결정할 것입니다.
높이와 바닥면 - 고전적 공식 (* - 곱셈 기호) :
S = 1 / 2 * b * h
예를 들어 숫자를 다음과 같이 대체 해 봅시다 : h = 16, b = 18, 우리는 다음을 얻습니다 :
S = 1 / 2 * 18 * 16 = 9 * 16 = 144;
이등변 삼각형의 면적은 S = 144cm2
우리를 도울 다른 수식이 있습니다.이등변 삼각형의 면적을 아는 법. 그러한 공식 중 하나는 헤론의 방법입니다. 복잡한 공식을 쓰지 말고, 근거로 다음과 같이 단축합니다 :
S = ¼ b √4 * a2-b2
b가 기초이고, - 동등한면이 분명하다. 이 공식은 높이가 알려지지 않은 경우에 적합합니다.
값을 a = 6, b = 3으로 대입하면 다음과 같이됩니다.
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
삼각형의 변과 같은 면적과 변의 각도를 계산하는 데 사용할 수 있습니다.
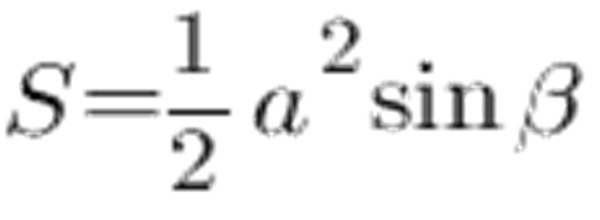
사인 테이블에 따르면, 45 °의 각도는 0.7071이고, 한 변의 각도는 6cm가됩니다. 다음을 얻습니다.
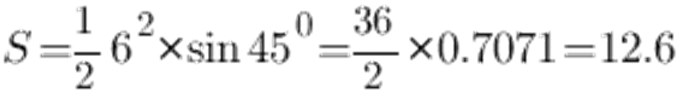
결과적으로 이등변 삼각형의 면적은 12.6 cm2입니다.
면적을 계산하는 방법은 다음과 같습니다.이등변 삼각형의 경우를 포함하지만 복잡한 수학의 개념에서 위에 주어진 것과 같은 "기본"계산에는 적용되지 않으며 다소 복잡합니다. 경험이있는 교사조차도 이해할 수없는 것들에 관해 이야기 할 가치가 없습니다.
그래서, 당신은 안도의 한숨을 쉬게 할 수 있습니다.이등변 삼각형의 면적을 찾기위한 작은 기하학 과정이 완성 된 것으로 간주되며 기사를 읽음으로써 얻은 지식은 "5"로 학습됩니다.